干渉計を超えて：曲率可変照明と位相回復が拓く、次世代非球面レンズ測定技術の深層解説

導入：高性能光学系の心臓部、「非球面」を測るという挑戦

なぜ今、非球面レンズが重要なのか？

現代の最先端光学システムにおいて、「非球面レンズ」はもはや不可欠な存在です。スマートフォンカメラ、AR/VRヘッドセット、衛星搭載の望遠鏡、そして高出力レーザー加工機に至るまで、その応用範囲は広がり続けています 1。球面レンズの組み合わせでは補正が困難だった収差（特に球面収差）を、たった一枚の非球面レンズで劇的に改善できるためです。これにより、光学システムの小型化、軽量化、そして高性能化が同時に達成されます 1。例えば、従来3枚から5枚の球面レンズで構成されていた光学系を、1枚の非球面レンズで置き換えることも可能になります 6。この性能要求は、宇宙望遠鏡のような極限環境から、デジタルプロジェクションや医療用内視鏡といった精密機器まで、あらゆる分野で高まっています 2。

製造現場のボトルネック：「測定」の壁

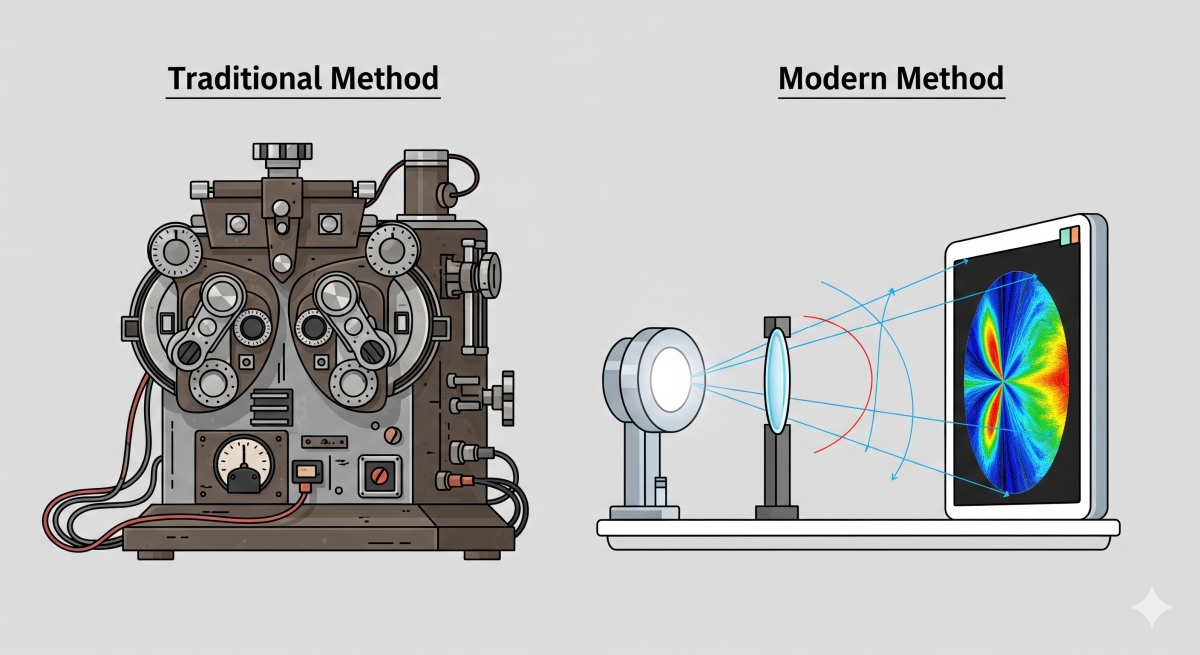
しかし、非球面レンズの価値は、そのナノメートルオーダーの表面形状精度に完全に依存します。そして、この極めて高い精度を保証するための「測定」こそが、製造における最大の課題、いわゆる「メトロロジー・ボトルネック」となっています。現在の業界標準（ゴールドスタンダード）は、レーザー干渉計です。これは極めて高い精度を誇る一方で、いくつかの重大な欠点を抱えています 1。第一に、システムが数千万円から一億円を超えることもあり、導入コストが非常に高いこと 7。第二に、測定対象の非球面形状に合わせて、高価な専用の補償光学素子（ヌルレンズやCGH）を都度設計・製作する必要があり、柔軟性に欠けること 1。そして第三に、参照光と測定光が異なる光路を通るため、振動や空気の揺らぎに極めて敏感であり、厳格な除振環境が必須となることです 9。

本記事の目的：計算の力で物理的制約を乗り越える新潮流

これらの課題は、高性能光学部品のイノベーション、特にAR/VRのような新しい市場を牽引するスタートアップにとって大きな障壁となっています。本記事では、Chengらが学術誌『Optics EXPRESS』で発表した論文 1 を基に、これらの課題を根本から解決する可能性を秘めた新しい測定法を深く掘り下げます。この技術は、高価な専用光学素子や厳格な環境制御を必要とせず、シンプルな構成で干渉計に匹敵する精度を目指すものです。本記事を通じて、読者は「位相回復」という計算イメージング技術の基本から、その最先端である「曲率可変照明」の革新性、そしてこの技術がもたらす産業へのインパクトまでを体系的に理解することができるでしょう。これは単なる技術改善ではなく、高精度な光学測定をより身近なものにし、新たな製品開発の可能性を解き放つ経済的な起爆剤となりうるのです。

基礎知識：なぜ「位相回復」が必要なのか？

光学測定における「位相問題」

光学素子の表面形状が理想からどれだけずれているかという誤差は、その素子を通過または反射する光の波面（Wavefront）の乱れ、すなわち「位相誤差」として現れます 10。この位相情報をナノメートルレベルで正確に捉えることが、形状測定の核心です。しかし、私たちが光を記録するために用いるCCDやCMOSといった光検出器は、光の強度（振幅の2乗）しか記録できません。波の「山」と「谷」のタイミングのズレである位相情報は、強度を記録した瞬間に失われてしまいます。これが、光学分野における古くからの難問、「位相問題」です 10。干渉計は、この問題を物理的に解決します。既知の完璧な参照波面と測定対象の波面を重ね合わせ、その干渉によって生じる縞模様（強度の濃淡）から、位相のズレを直接的に可視化するのです。

計算による解決策：反復位相回復法

位相回復（Phase Retrieval）は、干渉計のように物理的な参照波面を用いることなく、計算によって失われた位相情報を復元する技術です 12。その最も基本的なアルゴリズムの一つが、Gerchberg-Saxton (GS) 法です 15。これは、2つの異なる平面（例えば、物体が存在する面と検出器が置かれた面）における物理的な拘束条件を利用して、反復計算によって解を求める手法です。

まず、物体面での位相をランダムに仮定します。
この仮の波面を、フーリエ変換やフレネル回折といった物理法則に従って、検出器面まで数値的に伝搬させます 17。
検出器面で得られた計算上の波面の振幅を、実際に測定された強度画像の平方根に強制的に置き換えます。これが「強度拘束」です。
この拘束を適用した波面を、今度は逆方向に物体面まで伝搬させます。
物体面に戻ってきた波面に対し、既知の物理的制約（例えば、光が通過する領域の形状など）を適用します。
この一連のサイクルを何度も繰り返すことで、両方の平面での拘束条件を同時に満たすような、もっともらしい位相分布に徐々に収束させていきます 14。

従来法の限界：単一強度画像から多強度画像へ

GS法のような基本的な手法は、解が一意に定まらなかったり、計算が途中で誤った解（局所解）に陥って停滞（stagnation）してしまったりする問題がありました 1。この問題を克服するため、アルゴリズムに与える情報を増やすアプローチとして「多平面位相回復法」が主流となりました。これは、検出器を光軸に沿って複数回移動させ、異なる距離で複数の強度画像を記録する手法です 1。記録する画像が増えるほど、アルゴリズムが満たすべき拘束条件が増え、解の収束性と頑健性が向上します。

この技術の進化は、難しい問題を解くためには、より優れたアルゴリズムだけでなく、より情報量の多いデータを取得するための「測定方法の設計」そのものが重要であるという、計算イメージングにおける普遍的な原則を示しています。多平面法は「軸方向の多様性」をデータに与えましたが、それでもなお、収束速度や精度には課題が残されていました 1。

技術核心：曲率可変照明による画期的な情報取得

従来法との決定的違い：光源と検出器の同期移動

今回解説する論文の核心的な新規性は、単に検出器を動かすのではなく、点光源とCCDを一体として光軸に沿って同期移動させるという点にあります 1。この独創的な操作により、測定のたびに被測定素子に入射する光の波面の曲率が変化します。つまり、「異なる曲率を持つ球面波で素子を照らす（Varying-Curvature Illumination）」という、全く新しい情報取得方法を実現したのです。従来の多平面法が「伝搬距離」という単一のパラメータを変化させていたのに対し、本手法は「伝搬距離」と「入射波面の曲率」という2つのパラメータを同時に変化させます。これにより、アルゴリズムに与えられる情報の「多様性」が飛躍的に増大し、再構成問題の確実性を大幅に高めることができます。

なぜ収束が速く、精度が高いのか？

この手法の有効性は、シミュレーション結果に明確に表れています。従来の多平面法と比較して、同じ反復回数で再構成のRMS誤差が実に1/5にまで低減されることが示されました 1。この劇的な改善の背景には、照明の変調（Illumination Modulation）によって、被測定素子の位相情報がより多様な形で強度パターンにエンコードされるという原理があります 20。入射波面の曲率が変わると、素子の同じ箇所が異なる角度からの光線で照らされることになります。特に、非球面のように場所によって曲率が大きく異なる素子では、その微細な形状情報が強度変化として強調されやすくなります。これにより、アルゴリズムが局所解の罠から脱出し、真の解へと高速に収束することが可能になるのです。

このアプローチは、超解像顕微鏡で用いられる「構造化照明（Structured Illumination）」の考え方と通底しています。超解像顕微鏡が縞模様のような空間的なパターンを試料に照射することで、検出限界を超える微細構造の情報を可視化するのと同様に 23、本手法は曲率の異なる球面波という「軸方向の構造化照明」を用いることで、波面の微細な情報を強度パターンに埋め込んでいると解釈できます。これは、物理的な検出限界を、照明の工夫と計算処理の連携によって乗り越えるという、計算イメージングの強力な設計思想の現れです。

素子タイプに応じた専用アルゴリズムの構築

本手法のもう一つの重要な点は、測定対象に応じて最適化された2種類の再構成アルゴリズムを開発したことです 1。

反射型素子（非球面ミラー）用アルゴリズム: 光路が「点光源 → ミラー → CCD」と比較的シンプルです。アルゴリズムは、各測定位置jにおいて、入射球面波 $P_j$ と現在の推定変調関数 $T_n$ から出射波 $U_{n,j}$ を計算し、CCDまで伝搬させます。CCD面で強度拘束を適用後、逆伝搬させて $U'_{n,j}$ を得て、 $T$ を $T_{n+1} = U'_{n,j} P_j^*$ のように更新します 1。
透過型素子（非球面レンズ）用アルゴリズム: 光路が「点光源 → レンズ → ミラー → レンズ → CCD」と複雑で、光がレンズを2回通過します。この複雑な光路を正確にモデル化するため、より高度な更新手法が考案されました。更新は2段階で行われ、まず2回目のレンズ通過直後の出射波 $U^2$ に基づき、Wignerフィルターに似た方程式を用いて、レンズの変調関数 $T$ と、1回目の通過後にミラーで反射され2回目の入射となる波面 $Q$ の両方を更新します 1。次に、更新された $Q'$ を逆伝搬させて1回目の通過後の出射波 $U'^1$ を求め、これを用いて再度 $T$ を更新します。最終的に、これら2つの更新結果を平均化することで、より安定した推定値 $T_{n+1}$ を得ます 1。この専用アルゴリズムの存在が、実際の複雑な測定系における高い精度を保証する鍵となっています。

性能実証と従来技術との比較

実験による有効性の検証

本論文では、2つの異なるタイプの非球面素子を用いた詳細な実験により、提案手法の実用的な有効性を検証しています 1。

大型透過型非球面レンズ: 口径430mm x 430mmという非常に大きなレンズの測定において、業界標準である4D干渉計との比較が行われました。その結果、PV（Peak-to-Valley、波面の最大誤差）値の偏差は0.043λ（波長633nm換算で約27nm）と、極めて良好な一致を示しました 1。これは、複雑な光路を持つ透過型素子に対しても、専用に開発されたアルゴリズムが有効に機能し、高い精度を達成できることを証明しています。
反射型放物面ミラー: F値が3という、比較的曲率の急な（測定が難しい）非球面ミラーの測定では、干渉計とのPV値の差はわずか4.5nmであり、驚くほど高い精度が実証されました 1。
総合評価: 透過型・反射型の両方で、干渉計とのPV偏差が30nm未満という結果は、本手法が研究室レベルの概念実証に留まらず、実用的な高精度測定ツールとして十分な性能を持つことを強く示唆しています 1。

用語解説：「デジタルナイフエッジ」とは？

論文では、この手法を「デジタルナイフエッジ装置」に応用したと述べられています 1。この用語は、一般には刃物の角度を測る工具を指すため、混同を招く可能性があります 25。しかし、光学分野における「ナイフエッジテスト（フーコーテスト）」とは、1世紀以上前から存在する、レンズやミラーの収差を鋭敏に可視化する古典的な手法です。これは、焦点の近くにナイフの刃のような遮蔽物を置き、その影の動きから波面の傾きを観察するものです。従来のフーコーテストは定性的な評価に留まっていましたが、本研究における「デジタルナイフエッジ」とは、この

古典的でシンプルな光学系をベースに、位相回復アルゴリズムという計算の力を組み合わせることで、定量的で高精度な波面測定を可能にしたものを指します。既存のシンプルな装置に計算能力を付与することで、その価値を飛躍的に高めた好例と言えるでしょう。

技術比較：位相回復法 vs. 干渉法

本手法の真価を理解するため、業界標準であるフィゾー干渉法との比較を表にまとめます。この比較は、技術選択におけるビジネス上、またエンジニアリング上のトレードオフを明確にします。

特徴	曲率可変照明位相回復法（本手法）	フィゾー干渉法（業界標準）
測定原理	計算論的：回折強度パターンからの反復計算 1	物理的：参照波面との光波干渉 27
システムコスト	低い (点光源, カメラ, ステージ等の汎用品で構成) 1	非常に高い (高精度な参照平面/球面, 除振台が必須) 7
柔軟性	高い (素子ごとの専用補償光学系が不要) 1	低い (非球面ごとに専用のヌルレンズやCGHが必要) 1
環境耐性	高い (参照光不要の同軸光路のため振動・外乱に強い) 1	低い (非同軸光路のため振動や空気揺らぎに極めて敏感) 9
測定精度	高い (干渉計比でPV偏差<30nmを実証) 1	極めて高い (業界の精度ベンチマーク)
セットアップ複雑性	低い〜中程度	高い

この表が示す価値提案は明確です。究極的な精度では干渉計に一歩譲る可能性があるものの、コスト、柔軟性、環境耐性において圧倒的な優位性を持つことで、これまで高精度測定が困難だった多くの場面で新たなソリューションを提供します。

結論：広がるインパクトと今後の展望

計算イメージングという大きな潮流の中での位置づけ

本研究は、単独の優れた測定技術というだけでなく、より大きな技術的パラダイムシフトの一部として捉えるべきです。それは、「複雑で高価なハードウェア」への依存を減らし、「シンプルで安価なハードウェアと高度な計算処理」の組み合わせで課題を解決するという、計算イメージングの潮流です。この思想は、前述の超解像顕微鏡（SIM）23、フーリエタイコグラフィ、レンズレスイメージングなど、現代の光学分野における多くのブレークスルーと共通しています。物理的な光学素子の限界を、照明の工夫と計算アルゴリズムの力で乗り越えようとするアプローチなのです。

産業・ビジネスへのインパクト

高精度光学部品製造の民主化: 干渉計のような高額な設備投資なしに、ナノメートル級の品質管理が可能になることで、中小企業やスタートアップが高性能非球面レンズの製造市場に参入しやすくなります。
コスト削減とリードタイム短縮: 試作品ごとに高価なヌルレンズを設計・製造する必要がなくなるため、新製品開発のコストと期間が大幅に削減されます。これにより、新しい光学設計のイノベーションサイクルを高速化できます。
新たな応用分野の開拓: これまでコスト面で見送られていた民生品（例：次世代プロジェクター、ハイエンドVR/AR機器）への高性能非球面レンズの採用が進む可能性があります 2。また、製造ラインへのインライン測定や、加工機上でのオンマシン測定といった、従来は不可能だった応用も視野に入ります。

今後の展望と残された課題

本技術は大きな可能性を秘めていますが、さらなる発展に向けた課題も存在します。

自由曲面への拡張: 本研究は回転対称な非球面を対象としていましたが、今後の重要な課題は、より複雑な自由曲面（Freeform Optics）の測定への応用です。これには、アルゴリズムのさらなる高度化が求められます。
測定の高速化: 現状の反復計算は、リアルタイムのフィードバックにはまだ時間を要します。GPUコンピューティングの活用や、深層学習（AI）を用いた再構成アルゴリズムによる劇的な高速化が期待されます 30。
堅牢性の向上: 実環境における迷光や検出器ノイズなどへの耐性をさらに高めるため、正則化技術などを組み込んだアルゴリズムの改良が考えられます。

結論として、この「曲率可変照明位相回復法」は、シンプルさ、低コスト、高精度、そして高い拡張性を兼ね備えており、非球面光学素子の測定におけるゲームチェンジャーとなる潜在能力を秘めています。今後の発展が、光学産業全体の進化を加速させることは間違いないでしょう。